Historia de la geometría 3: geometría no Euclideana

Durante 2000 años muchos matemáticos dedicaron su tiempo y sus esfuerzos a completar con nuevos teoremas esa gran construcción que es la geometría de Euclides. Algunos de ellos trataron de reducir el número inicial de postulados, pues se pensaba que el 5º postulado podía demostrarse a partir de los otros cuatro. Es decir, querían convertir el 5º axioma en teorema, en cuyo caso bastaría aceptar los cuatro primeros axiomas y tomarlos como punto de partida para obtener finalmente la misma geometría.

De la misma forma que un arquitecto calcula los cimientos precisos para que la torre que desea construir sea lo más esbelta posible, así hacen los matemáticos cuando buscan los axiomas más convenientes para su teoría y, cuantos menos axiomas utilicen, más elegante será el resultado final.

Para convertir el 5º postulado en un teorema, era necesario obtener una demostración, y a ello se dedicaron sin éxito muchos matemáticos a lo largo de varios siglos. Fue a principios del siglo XIX cuando tres matemáticos, Lobachevski en Russia, Gauss en Alemania y Bolyai en Hungría, dieron con un resultado inesperado que arrojó una nueva luz sobre esta cuestión. Trabajaron independientemente unos de otros en la elaboración de modelos geométricos que mantenían los cuatro primeros postulados de Euclides a la vez que negaban el quinto. Esperaban que una geometría en la que se negara que "por un punto exterior a una recta pasa una única paralela", sería una geometría incoherente y llena de contradicciones.

Existen diversas propuestas y tipos de Geometrías no Euclidianas, algunos ejemplos son: Geometría Hiperbólica, Geometría Esférica. Las Geometrías no Euclidianas son muy importantes para el desarrollo de la Física, específicamente en la Astronomía. También es fundamental para conocer el Universo matemático, ampliar el Horizonte de dos y tres dimensiones a un posible Universo de n dimensiones.

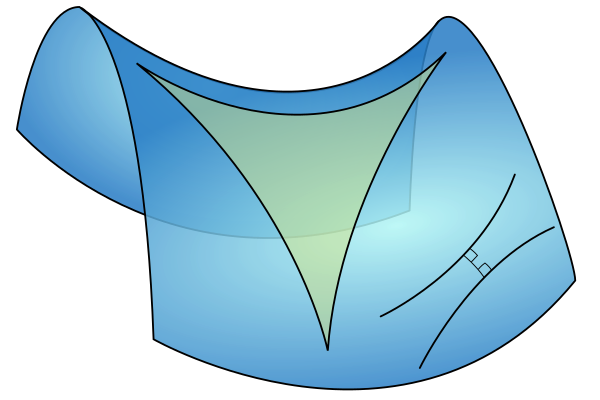Un triángulo en una superficie con forma de una silla de montar (un paraboloide hiperbólico), así como dos rectas paralelas divergentes. Fuente

Historia de la geometría II: Los postulados de la geometría Euclidea

Los postulados de Euclides que se incluyen en "Los Elementos", obra de la cual hablamos en la última entrada del blog, dan lugar a la geometría que todavía hoy conocemos con el nombre de Geometría Euclideana. 

La presentación tradicional de la geometría euclidiana se hace en un formato axiomático, en el que todos los teoremas («declaraciones verdaderas») derivan de un pequeño número de axiomas.​ Un sistema axiomático es aquel que, a partir de un cierto número de proposiciones que se presuponen «evidentes» (conocidas como axiomas) y mediante deducciones lógicas, genera nuevas proposiciones cuyo valor de verdad es también lógico.

Euclides planteó cinco postulados en su sistema:

1. Dados dos puntos se puede trazar una recta que los une.
2. Cualquier segmento puede prolongarse de manera continua en cualquier sentido.
3. Se puede trazar una circunferencia con centro en cualquier punto y de cualquier radio.
4. Todos los ángulos rectos son congruentes.
5. Si una recta corta a otras dos formando, a un mismo lado de la secante, dos ángulos internos agudos, esas dos rectas prolongadas indefinidamente se cortan del lado en el que están dichos ángulos.

Representación geométrica de los postulados de Euclides.

Historia de la geometría I: Euclides

Euclides nació cerca del 325 a.C y murió hacia el 265 a.C. en Alejandría, ciudad situada al norte de lo que actualmente es Egipto. Fue un matemático griego cuya obra principal, "Elementos de geometría", es un extenso tratado de matemáticas en 13 volúmenes sobre materias tales como geometría plana, proporciones en general, propiedades de los números, magnitudes inconmensurables y geometría del espacio. Probablemente estudió en Atenas con discípulos de Platón. Enseñó geometría en Alejandría y allí fundó una escuela de matemáticas.

Los Elementos

Los Elementos de Euclides se utilizaron como libro de texto durante 2.000 años, e incluso hoy, una versión modificada de sus primeros libros constituye la base de la enseñanza de la geometría plana en las escuelas secundarias. La primera edición impresa de las obras de Euclides que apareció en Venecia en 1482, fue una traducción del árabe al latín.

En dicha obra se presenta de manera formal, partiendo únicamente de cinco postulados, el estudio de las propiedades de líneas y planos, círculos y esferas, triángulos y conos, etc.; es decir, de las formas regulares. Probablemente ninguno de los resultados de Los elementos haya sido demostrado por primera vez por Euclides pero la organización del material y su exposición, sin duda alguna se deben a él. De hecho hay mucha evidencia de que Euclides usó libros de texto anteriores cuando escribía Los Elementos.

Uno de los fragmentos más antiguos que se conservan de la obra de Euclides.
Fue encontrado en Oxirrinco y data del año 100 D.C.
 Fuente: Universidad de la Columbia Británica

Teselados III: ¡Hazlo tú mismo!

Ha llegado la hora de hacer tus propios teselados utilizando lo que aprendimos en las entradas anteriores. Te proponemos la herramienta "Tessellation artist" que hemos encontrado en el sitio web www.mathisfun.com.

Enlace a "Tessellation artist"

Es algo difícil de utilizar al principio pero el manejo es bastante intuitivo y podrás crear tus propias teselaciones en un par de minutos. Se pueden utilizar polígonos regulares, círculos, líneas, e incluso hay una herramienta de dibujo a mano alzada. Simplemente dibuja una forma y a continuación arrastra los puntos rojo y azul para variar la posición y el ángulo. Además, el programa te permite la opción de imprimirlo.

Te mostramos a continuación un teselado que hemos creado a partir de hexágonos regulares y rombos, aunque seguro que puedes hacer diseños más complejos con algo más de tiempo.

Teselados II: Teselados semirregulares

Hemos visto que Los términos teselaciones y teselado​ hacen referencia a una regularidad o patrón de figuras que recubren o pavimentan completamente una superficie plana que cumple con dos requisitos:
     1.Que no queden espacios.

     2.Que no se superpongan las figuras.

Además, los teselados regulares que estudiamos en la entrada anterior están formados exclusivamente por polígonos regulares: triángulos, cuadrados y hexágonos. Veamos ahora un tipo de teselados algo más complejos.

Teselados semirregulares

Una teselación semirregular está hecha con dos o más polígonos regulares. ¡El patrón debe ser el mismo en todos los vértices! Para darle un nombre a una teselación, nos situamos en un vertice y damos la vuelta anotando cuántos lados tiene cada polígono en orden... por ejemplo "3.12.12". Y siempre se empieza por un polígono que tenga el mínimo número de lados, así que es "3.12.12", no "12.3.12".

Sólo existen ocho teselaciones semirregulares, te mostramos a continación la llamada 3.3.4.3.4 (fuente:Wikimedia Commons):

Teselados I: Teselado regular

Definición de teselado

Vamos a ver ahora un tema que está muy relacionado con los movimientos que estudiamos en las entradas anteriores del Blog: las teselaciones o teselados.

Un teselado o teselación​ consiste en una regularidad o patrón de figuras que cubren completamente una superficie plana, de manera que no quedan espacios ni tampoco se superponen las figuras.

Los teselados se crean usando transformaciones isométricas (sin variar las dimensiones ni el área) sobre una figura inicial, es decir, copias idénticas de una o diversas piezas o teselas con las cuales se componen figuras para recubrir totalmente una superficie. Vamos a fijarnos en primer lugar en el teselado más básico que es el teselado regular, en el que se utiliza solo un tipo de polígono regular.

Teselado regular

Pues bien, solo son posibles teselados regulares empleando triángulos equiláteros, cuadrados y hexágonos regulares. Con un pentágono regular, por ejemplo, no se puede. ¿Y por qué solo triángulos equiláteros, cuadrados y hexágonos regulares? Si lo pensamos un poco, la razón es bastante sencilla.

Si queremos cubrir todo el plano sin solapamientos ni huecos, en un vértice cualquiera del teselado la suma de los ángulos interiores de los polígonos que tienen ese vértice en común debe ser de 360º.

Dado que, como he comentado antes, el teselado regular se hace con un único tipo de polígono regular, dicho polígono debe tener un ángulo interior que sea divisor de 360º. Pues ocurre que los únicos polígonos regulares cuyos ángulos interiores son divisores de 360º son el triángulo equilátero (60º), el cuadrado (90º) y el hexágono regular (120º). Te lo enseñamos en el siguiente video:

Movimientos en el plano IV: Composición de movimientos

Cuando se aplican a una misma figura varios movimientos se dice que se ha hecho una composición de movimientos. Un movimiento compuesto puede estar formado por cualquier combinación de los movimientos que ya hemos visto. Por ejemplo podemos realizar:

• dos traslaciones
• tres giros
• un giro y una traslación
• Una traslación, un giro y una simetría axial

La composición de movimientos es otro movimiento pues conserva la forma y el tamaño de las figuras.

Práctica

Vamos a utilizar nuevamente el applet GeoGebra para analizar un movimiento compuesto formado por una traslación y una simetría axial. Te proponemos que sigas los siguientes pasos:

     1. Marca la casilla Traslación para ver el primer movimiento.
     2. Marca a continuación la casilla Simetría para ver el segundo movimiento.
     3. Con las dos casillas marcadas, modifica el vector u y la dirección del eje para ver distintas variantes de esta composición.

Movimientos en el plano III: Simetrías

Llegamos a la tercera parte de esta serie de cuatro entradas en la que abordaremos los llamados movimientos en el plano.

A estas alturas deberías estar familiarizado con el manejo del applet GeoGebra y con los dos primeros movimientos que estudiamos: traslación y giro. Si no es así, te recomiendo que vuelvas a la primera entrada de la serie y sigas practicando, ya que este movimiento es algo más complejo que los anteriores. Si ya tienes suficiente práctica, te propongo que realices el ejercicio a continuación para experimentar con las simetrías.

Teoría

Se llama simetría axial S, de eje e, a un movimiento que transforma un punto P en otro P' de modo que e es mediatriz del segmento PP', o lo que es lo mismo, d(P, e) = d(P', e).

Práctica

En el siguiente applet aparece un triángulo, crea un eje y aplica una simetría axial. Los pasos a seguir son:

     1. Primero debemos crear el eje de simetría. Selecciona el 3er icono de la esquina superior izquierda y selecciona los dos puntos por los que pasa el eje de simetría.

     2. Haz click sobre el 5to icono de la esquina superior izquierda y selecciona la opción "Simetría axial".
     3. Haz click sobre el triángulo y a continuación haz click nuevamente sobre el eje de simetría que definimos en el primer paso.

Movimientos en el plano II: Giros

Llegamos a la segunda parte de esta serie de cuatro entradas en la que abordaremos los llamados movimientos en el plano.

Si no has tenido problemas para superar la primera actividad, ya estarás familiarizado con el applet GeoGebra. Te propongo un nuevo ejercicio para seguir experimentado con el movimiento de giro.

Teoría

Se llama giro de centro O y ángulo ß a un movimiento que hace corresponder a cada punto P otro punto P' tal que : d(O, P) =d (O, P') y ángulo(POP') = ß. Cuando el ángulo de giro es de 180º se dice que es una simetría central de centro O.

Práctica

En el siguiente applet aparece un triángulo, crea un punto y aplica un giro con centro de rotación en ese punto. Haz que se muestre el ángulo de rotación. Los pasos a seguir son:

     1. Selecciona el 5to icono de la esquina superior izquierda y elige la opción "giro". 

     2. Haz click sobre el triángulo para seleccionarlo.

     3. Haz click sobre la pantalla para definir el centro del giro. En la ventana de diálogo que se abre, introduce el ángulo del giro y el sentido (horario o anti-horario).
     4. Para hacer que se muestre el ángulo de rotación, selecciona el 4to icono de la esquina superior izquierda. A continuación haz click sobre un punto cualquiera del primer triángulo, click otra vez sobre el centro de giro, y un último click sobre el punto análogo al primer punto seleccionado, pero esta vez del segundo triángulo.

Movimientos en el plano I: Traslaciones

En esta serie de cuatro entradas abordaremos los llamados movimientos en el plano.  Un movimiento en el plano es una transformación geométrica del plano que conserva los ángulos y las distancias (la forma y el tamaño). Se distinguen tres tipos de movimientos: Traslación, giro y simetría.

Para poder experimentar y facilitar el aprendizaje, contaremos con la ayuda de un applet que nos permitirá estudiarlos de una forma muy gráfica e interactiva.

Teoría

Como seguramente habremos estudiado en clase, Se llama traslación T de vector libre AB a una transformación que asocia a cada punto P del plano otro punto P'=T(P) de manera que el vector PP' sea igual al vector AB.

Práctica

En el siguiente applet aparece un triángulo, crea un vector y aplica una traslación. Los pasos a seguir son:

     1. Selecciona el 5to icono de la esquina superior izquierda y elige la opción traslación. 

     2. Haz click sobre el triángulo para seleccionarlo.
     3. Define el vector libre de la traslación haciendo un click en cualquier sitio de la pantalla para seleccionar el primer punto, y un segundo click para seleccionar el punto final.